<기하학원론> 다섯번째 후기
곰곰
2023-09-04 01:47
201
우리는 드디어 1권 명제로 들어갔고 지난 시간에 이어 작도를 하고 있다. 앞서 얘기했듯, 여러 유명인사들이 그-렇게 유클리드에 빠져들었다는 것이 살짝 이해될 것 같기도 하다. 작도를 하고 명제가 잘 증명되면 묘한 짜릿함이 있었던 것이다! (안타깝게도 술술 증명되는 경우가 많진 않아서 순간의 감동일뿐, 몰입의 경지는 요원하다...) 어쨋든 우린 명제 30 까지 읽고 (살짝 들뜬 마음으로?) 만났다. ㅋ
명제16. 모든 삼각형에 대하여 변들 중 하나가 연장되면서, 외각은 반대쪽 내각들 각각보다 크다.
주어진 삼각형 ABC의 반직선 BC 위의 점이면서 선분 BC의 밖의 점을 점 E라고 하자. 그러면, 외각ACD은 맞은편에 있는 두 내각 CBA와 BAC보다 크다는 것을 보이자.

AC를 점 E에서 이등분하고 [1권 명제10] BE를 이으면서 F로 직선으로 연장하고 BE와 같게 EF가 놓이고 [1권 명제3] FC를 잇고 [공리1] AC를 G로 더 긋는다.[공리2]
삼각형 AEB와 CFE에서 AE=EC,BE=EF 이므로,∠AEB=∠FEC이다. [I권-명제 15] 따라서 삼각형 AEB와 CFE는 합동이다.
그러므로 AB=FC, ∠BAE=∠ECF이고 [I권 명제 4],∠ECD >∠ECF이다. [일반개념 5] 따라서∠ACD >∠BAE이다.
같은 방법으로 선분 BC를 이등분하면∠BCG >∠ABC,∠BCF =∠ACD을 증명할 수 있다. [I권 명제 15]
그러므로 주어진 삼각형의 한 변의 한 쪽을 연장하여 만들어진 외각은 맞은편 두 내각보다 크다. Q.E.D.
명제18. 모든 삼각형에 대해 더 큰 변은 더 큰 각을 마주한다.
주어진 삼각형 ABC에서 변 AC의 길이가 변 BC보다 길다. 그러면 변 AC의 대각인 각 BCA보다 크다는 것을 보이자.

삼각형 ABC에서 AC > AB 이라고 하자. 변 AC 위에 AB=AD가 되도록 점D를 잡는다. [1권 명제3] 그러면,
∠ADB > ∠ACB [1권 명제16]
∠ABD = ∠ADB [1권 명제5]
∠ABC > ∠ABD [일반개념 5]
이므로 ∠ABC = ∠ACB 이다. 그러므로 삼각형에서 더 긴 변의 마주보는 대각의 크기도 크다. Q.E.D.
명제 20. 모든 삼각형에 대하여 두 변(의 합)은, 어떻게 함께 잡든, 남은 변보다 크다.
주어진 삼각형 ABC가 있다. 그러면 삼각형 ABC에서 두 변의 길이의 합은 나머지 한 변의 길이보다 크다는 것을 보이자.
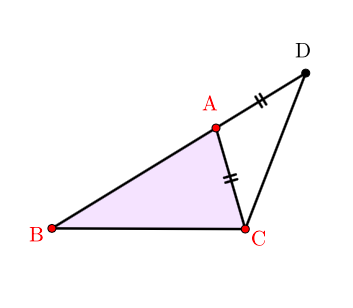
변 BA 위에 AC = AD가 되도록 점 D를 잡는다. [1권 공리2, 명제3] 선분 DC를 긋는다. (1권 공리1]
삼각형 ADC가 이등변삼각형이므로, ∠ACD = ∠ADC 이다.
또한 ∠BCD = ∠BCA + ∠ACD 이다. [1권 명제5, 일반개념 5]
그러므로 ∠BCD > ∠ACD
따라서 [1권 명제19]에 의해 삼각형 BCD에서 BD > BC 이 성립한다.
또한 DA = AC 이므로 AB + AC > BC 가 성립한다.
같은 방법으로 AB + BC > CA 와 BC + CA > AB 인 경우에도 같은 방법으로 보일 수 있다. 그러므로 주어진 삼각형에서 두 변을 더한 길이는 나머지 한 변의 길이보다 더 길다. Q.E.D.
이것에 대해 <해설서>는 3가지 증명방식을 보여준다. 헤론과 포피리는 변을 늘리지 않고 삼각형 안에다 점 D를 잡고 증명했고,

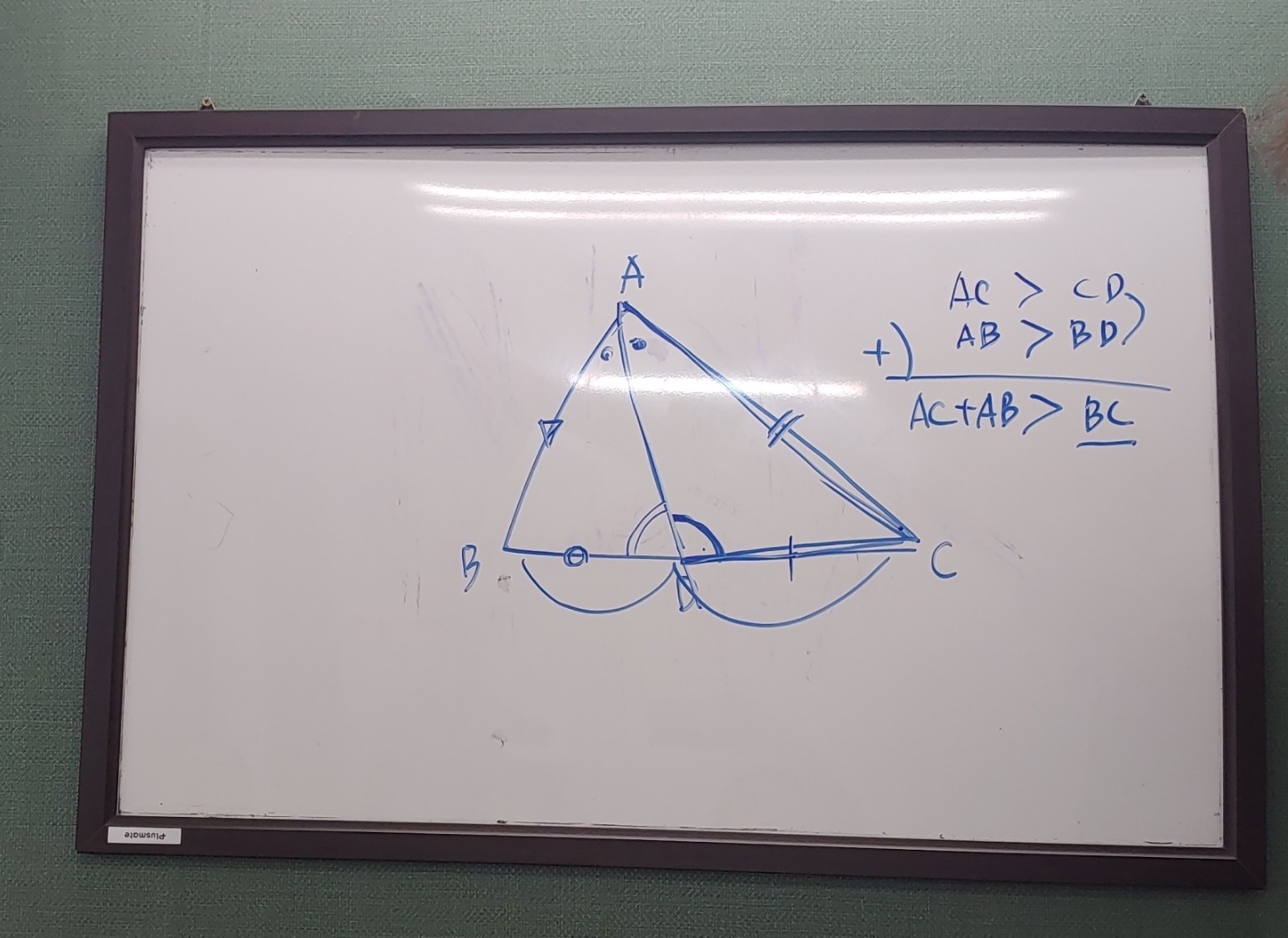
정삼각형, 이등변삼각형, 부등변삼각형의 경우로 나누어 각각 증명하는 방식도 있었으며,

모순을 이끌어내는 방법으로 증명을 하는 방식도 있었다.

반면, 에피쿠로스 학파 사람들은 이 명제가 아주 명백해 당나귀들도 알고 있으니, 증명할 필요가 없다고 놀려댔다고 한다. 그 증거는, 삼각형의 한 꼭지점에 풀을 놓고 다른 한 꼭지점에 당나귀를 놓으면 당나귀는 풀을 먹기 위해 삼각형의 한 변을 따라 똑바로 움직인다. 절대로 두 변을 따라 돌지 않는다! 하지만 프루클루스는 이것에 대해 어떤 법칙이 옳다는 개념을 갖는 것과, 그걸 과학적으로 증명하고 ‘왜’ 그게 옳은지 아는 것은 다른 일이라 답하였다. 그리스 시대의 이러한 증명은 과연 논리의 계단을 하나씩 하나씩 밟아 올라가는 과정이었다.
유클리드는 증명을 마친 후 언제나 Q.E.D.(Quod Erat Demonstrandum)라는 라틴어 낱말을 썼다고 한다. 퀴드 에라트 데몬스트란둠. 흔히 “이로써 증명되었다”라고 알려져 있지만, 직역하면 “이것이 보여져야 할 것이었다”라 한다. 그가 ‘보여져야 할 것’이 말한 것도 바로 이것이 아닐까. 그리고 우리가 꾸역꾸역 <원론>을 잡고 읽어가는 이유도… … ? ㅎㅎ
명제 17 에서 프로클루스는 변을 길게 늘이는 일이 꼭 필요한 것이 아니라며, 바깥각을 반드시 만들어야 할 이유가 없다고 얘기하며 이런 관점에 따라 삼각형의 변을 늘이지 않은 채 이 명제를 증명하려고 시도하기도 했다. 명제 19 을 드모건은 별도의 작도 없이 논리적으로 증명해 내기도 한다. 유클리드는 ‘여러 경우들로 나눠서’ 모순을 이끌어내는 방법으로 증명한다. 다른 가정들에 따라서 여러 경우들로 나눠서, 각각의 경우들이 증명하려는 법칙과 어긋나도록 만든 다음, 이 경우들이 생길 수 없음을 보이는 것이다. 한 직선이 다른 직선보다 길지 않으면, 그것은 길이가 같거나 아니면 더 짧은 것이다.
<해설서>에 따르면 유클리드를 비롯해 위대한 그리스 기하학자들은, 가능한 경우들을 모두 다루어 놓지 않았으며, 가장 어려운 경우만을 다루어 놓고, 나머지 경우들은 독자들이 직접 해결하도록 남겨두는 게 보통이었다고 한다. 그렇기 때문에 여러 세대를 거친 <원론>의 오랜 전승 과정에서 많은 독자들(수학자들)의 반응이 축적될 수 있었던 것일 수 있겠다는 생각이 든다. 그렇게 지금의 독자인 우리는 유클리드 <원론>만을 읽는 것이 아니라 앞선 시대의 독자들이 원론을 어떻게 읽었는지 그 반응, 그 역사까지도 함께 읽을 수 있게 된 것 같아서. (물론 그것이 우릴 힘들게 하긴 하지만… ㅋ )
정리하자면, 1권의 첫번째 부분, 즉 명제 26까지는 주로 삼각형을 다루었다. 삼각형들을 만드는 방법, 변과 각의 상호작용, 여러 삼각형들이 있을 때, 그들의 변과 각의 크기에 따른 비교, 그리고 합동인 삼각형들의 넓이 비교. 그리고 두번째 부분(명제 27-34)은 세번째 부분(명제35-48)으로 넘어가는 관문으로, 세번째 부분에서 다룰 삼각형들의 넓이, 평행사변형들이나 정사각형들의 넓이 같은 새로운 개념을 다루기 위해 필요한 것들이 나온다. 세번째 부분을 위해선 평행선을 사용하는 게 꼭 필요하고, 두번째 부분에선 평행선 이론을 확립하고 있다.
처음엔 뭔가 증명이 잘 될 것 같아서 들떴었는데, 역시나 실제로 해보니 정리가 잘 안 됐다. 하지만 셋이서 머리를 맞대니 훨씬 좋다는 것만은 확실했다. ㅋㅋ 우리는 다음 시간 명제 48번까지, 1권을 모두 읽고 오기로 했다. 화이팅!
| 번호 | 제목 | 작성자 | 작성일 | 조회 |
| 487 |
<세계 끝의 버섯> 2부 후기
(6)
호수
|
2023.12.28
|
조회 208
|
호수 | 2023.12.28 | 208 |
| 486 |
<세계 끝의 버섯> 1회차 후기
(3)
동은
|
2023.12.26
|
조회 272
|
동은 | 2023.12.26 | 272 |
| 485 |
<세계 끝의 버섯> 번개세미나 모집합니다! (4회)
(11)
동은
|
2023.11.26
|
조회 878
|
동은 | 2023.11.26 | 878 |
| 484 |
<기하학원론> 아홉번 째 후기 - 삼각형은 위대하다
(2)
여울아
|
2023.10.04
|
조회 172
|
여울아 | 2023.10.04 | 172 |
| 483 |
<기하학원론> 여덟번째 후기 - 이제 '원'인가요
(1)
곰곰
|
2023.09.25
|
조회 187
|
곰곰 | 2023.09.25 | 187 |
| 482 |
<기하학원론>일곱번째 후기-작도는 상상이 아니다
(3)
여울아
|
2023.09.19
|
조회 218
|
여울아 | 2023.09.19 | 218 |
| 481 |
<기하학원론> 여섯번째 후기
(3)
진공묘유
|
2023.09.12
|
조회 215
|
진공묘유 | 2023.09.12 | 215 |
| 480 |
<청년, 루크레티우스를 만나다> 저자 민호와의 만남의 자리! 후기입니다~
(2)
동은
|
2023.09.06
|
조회 221
|
동은 | 2023.09.06 | 221 |
| 479 |
<기하학원론> 다섯번째 후기
(2)
곰곰
|
2023.09.04
|
조회 201
|
곰곰 | 2023.09.04 | 201 |
| 478 |
<기하학 원론> 네 번째 후기 - 연속의 원리
여울아
|
2023.08.29
|
조회 156
|
여울아 | 2023.08.29 | 156 |
| 477 |
<청년, 루크레티우스를 만나다> 저자와의 만남에 초대합니다~ (8/31)
(2)
고은
|
2023.08.24
|
조회 805
|
고은 | 2023.08.24 | 805 |
| 476 |
<기하학 원론> 세번째 후기
(2)
진공묘유
|
2023.08.22
|
조회 177
|
진공묘유 | 2023.08.22 | 177 |

ㅋㅋ 그래요. 우리에겐 화이팅이 필요해~
여울아샘 화이팅 !!!!