<기하학원론> 아홉번 째 후기 - 삼각형은 위대하다
여울아
2023-10-04 15:12
173
이번 후기는 쓰기도 전에 제목부터 떠올랐어요.
삼각형은 위대하다? 피타고라스 만세?
지난 시간 곰곰의 후기에서 처럼 우리는 겨우 제3권 "원"에 접어들었는데, 웬 삼각형?
명제 14. 원 안에서, 같은 직선들은 심으로부터 같게 떨어져 있고, 중심으로부터 같게 떨어져 있는 직선들은 서로 같다.
첫 단계는 선분 AB와 CD가 중점으로부터 떨어진 거리가 같다는 것을 증명해야 한다.
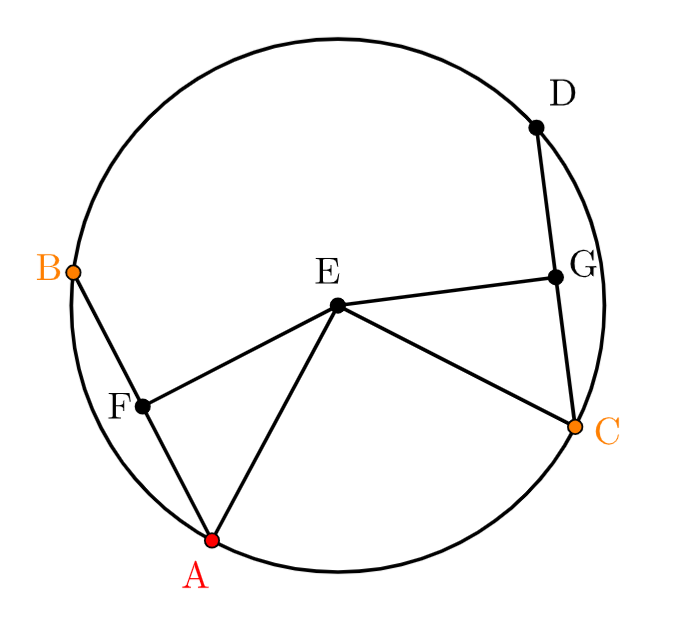
먼저 중점을 찾자. 이것은 3권 명제1번에서 아무 선이나 긋고 이 선분을 이등분하는 점(F, G)을 찾아야 한다. AB와 CD와 수직이 되도록 EF와 EG를 잇는다. 그리고 선분 EA 와 EC를 잇는다. 그러면 EF는 AB를 이등분하고 EG는 CD를 이등분한다. 이들 EF와 AF로 만든 사각형은 EG와 CG로 만든 사각형과 넓이가 같다. 왜냐하면 AF와 CG는 길이가 같기 때문. EF와 EG 도 마찬가지. 정의4에 의하면 원의 중점에서 수직이 되도록 그은 선들은 길이가 같으면 중점으로부터 같은 거리에 있다. 따라서 AB와 CD는 같은 거리이다.
다음 단계는 AB와 CD가 길이가 같다는 것을 증명해야 한다. AB는 AF의 두 배. CD는 CG의 두 배. 제1권 명제47에 의하면 이다. 다시 말해서 EF와 AF로 만든 정사각형들은 EA로 만든 정사각형과 넓이가 같다. 이것이 삼각형 넓이에 대한 피타고라스의 정리이다. 여기서 EF와 EG로 만든 정사각형이 같고, AF와 CG로 만든 정사각형이 같다. 그러므로 이들 각각 길이가 같다. AB는 AF의 두 배이고, CD는 CG의 두 배이므로 AB와 CD는 길이가 같다.
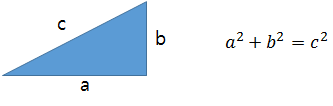
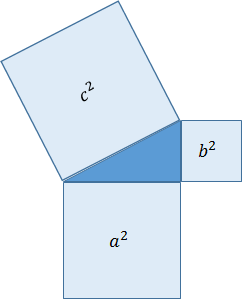
ㅎㅎ 원 안에서도 결국 피타고라스의 정리를 이용해서 넓이를 구하는 구나.. 싶으니, 진공묘유님이 세미나에서 제1권을 끝내고 났을 때 피라미드 얘기를 했던 게 생각나더군요. 처음부터 피라미드가 지금의 모양은 아니었다. 이렇게도 해보고 저렇게도 해보는 과정에서 현재의 삼각형 모양이 되었다는 얘기였어요. 그렇다면 고대에는 삼각형이 가장 안정적인 조형물이었기 때문이 아닐까 이런 얘기도 나누었지요. 제2권에서는 평행사변형의 넓이, 길이에 관한 증명을 다룰 때도 가장 많이 쓰이는 방법은 어떻게든 쪼개서 삼각형의 성질을 이용하는 것이었구요. 이제 원에 이르러서도 삼각형의 성질을 이용하는 것이 중요한 키포인트라니...
명제15. 원 안에서, 최대 직선은 지름이고, 다른 것들 중에서는 중심에 가까운 직선이 먼 직선보다 항상 더 크다.
원 안에 삼각형 파티를 좀더 즐겨보자. 이제 원 안에 지름이 가장 긴 직선이라는 것을 증명하기 위해 삼각형들이 등장한다.
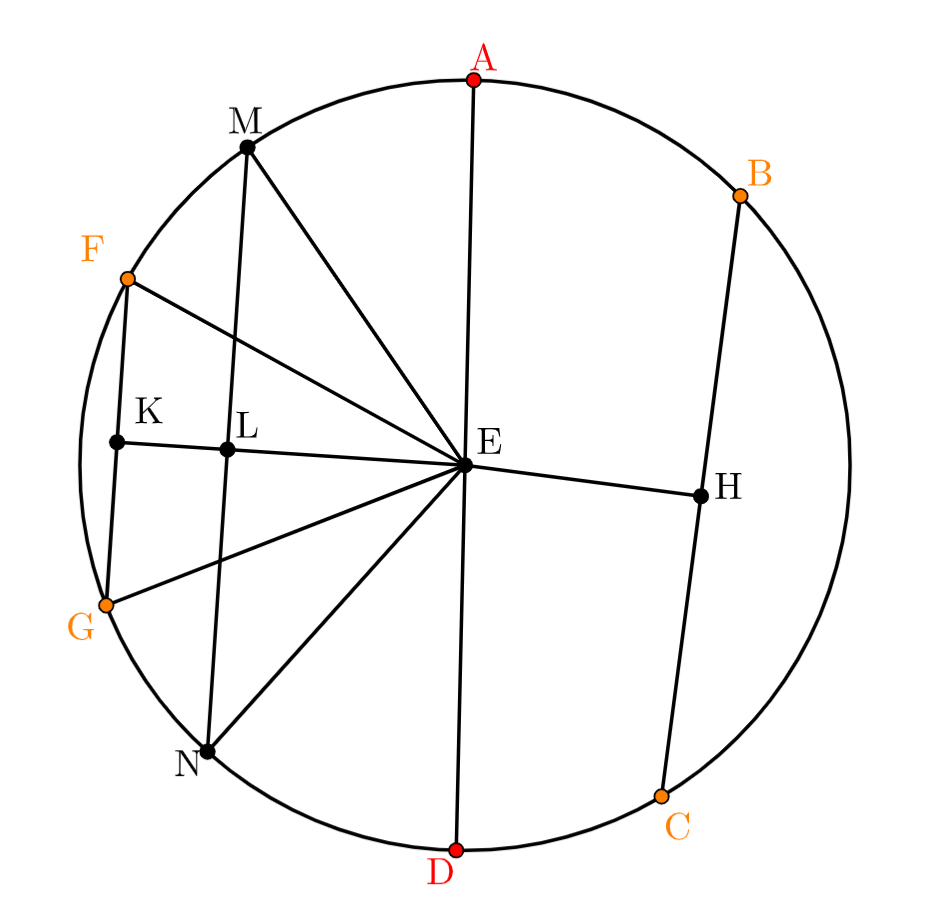 원AD가 지름이고 E가 중점이라고 하자. BC는 중점E에서 가장 가까운 선분이라고 하자. 반대로 FG는 가장 먼 선분이라고 하자. 그러면 지름 AD가 가장 길고, 그 다음은 BC, 가장 짧은 선은 FG임을 증명해야 한다.(AD>BC>FG 임을 증명하라)
원AD가 지름이고 E가 중점이라고 하자. BC는 중점E에서 가장 가까운 선분이라고 하자. 반대로 FG는 가장 먼 선분이라고 하자. 그러면 지름 AD가 가장 길고, 그 다음은 BC, 가장 짧은 선은 FG임을 증명해야 한다.(AD>BC>FG 임을 증명하라)
먼저 중점으로부터 BC와 수직이 되도록 EH를 잇는다. 마찬가지로 FG와 수직이 되도록 EK를 잇는다. 그러면 정의5에 의해 원의 중점으로부터 멀수록 선분이 짧기 때문에 중점에서 가까운 BC를 잇는 EK는 EH보다 더 길다. EL과 EH는 같은 거리가 되도록 잡는다. 이 선에 수직이 되도록 MLN을 잇는다. 그리고 선분 ME, EN, FE, EG를 그어서 쪼개라. 그러면 EH와 EL의 길이가 같고, BC와 MN의 길이도 같다. AE는 EM과 같고, ED는 EN과 같으니, AD는 EM과 EN을 합한 것과 같다. 그러면 삼각형 비례관계에 관한 1권 명제20에 의해 EM과 EN을 더한 것은 MN보다는 길다. MN과 BC는 길이가 같으므로 AD는 BC보다 길다.
원의 반지름에 해당하는 나머지 모든 선분들(EF, EG)도 마찬가지이다. 각 MEN은 각FEG보다 크다. 이것은 제1권 명제24에 의해 각이 크면 밑변도 크기 때문에, MN은 FG보다 더 길다. 따라서 AD>BC>FG 순으로 더 길다.
여기서도 키포인트는 더 큰 각을 가진 삼각형의 밑변의 길이가 더 길다는 성질을 이용한 것이다. 그림은 복잡해보이지만 원리는 의외로 간단하다. 어떻게든 수직선을 잇고 쪼개서 삼각형을 만들어 그 성질을 이용해서 증명하는 것이다.
마지막으로 작도의 묘미를 살리는 명제를 소개하고자 한다. 이 명제는 여기서 딱 한 번 쓰였고, 책 어디서도 다시 불리지 않는 것으로 봐서는 이 명제 그 자체는 큰 의미가 없다고 봐야한다고 해설자는 설명한다.
명제16. 원의 지름 끝에서 그 지름과 직각으로 그어진 직선은 원 외부로 떨어질 것이다. 또 직선과 둘레 사이의 공간을 가로질러 어떤 다른 직선이 끼어들 수 없다. 또 반원의 각은 어떤 직선 예각보다 크고, 남은 각은 (어떤 직선 예각보다) 작다.
- 이 명제를 다 알 필요가 없다!!(오늘날 쓰이지 않으니까..) 여기서 말하는 예각은 소위 "뿔처럼 뾰족한 각" 혹은 "섞인 각"이라고 불린다. 왜냐? 원과 그 접선이 만나기 때문이다. 둥근 부분과 직선이 만나 뾰족한 각을 이룬다고 해서 붙여진 이름들이다. 이 당시는 이렇게 섞인 각을 사용하는 것이 널리 퍼져 있었다고 추측된다. 그런데 처음엔 이 명제에 근거한 작도가 이해되지 않았다.
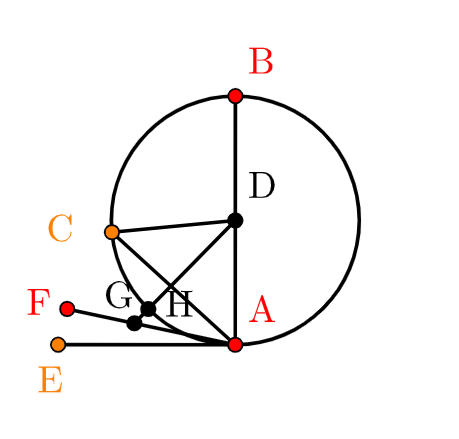
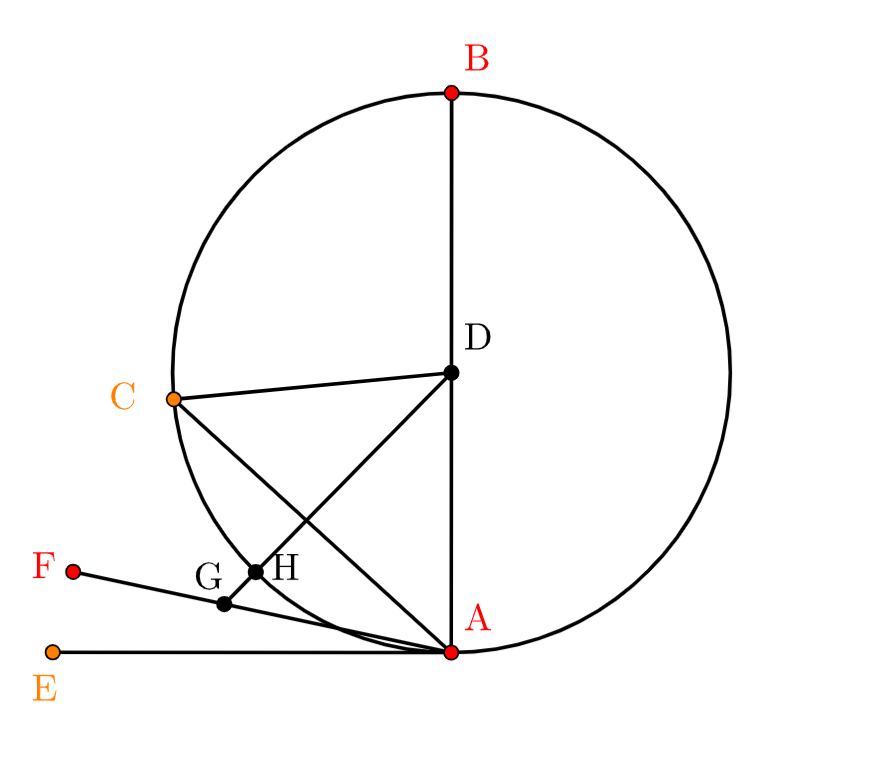
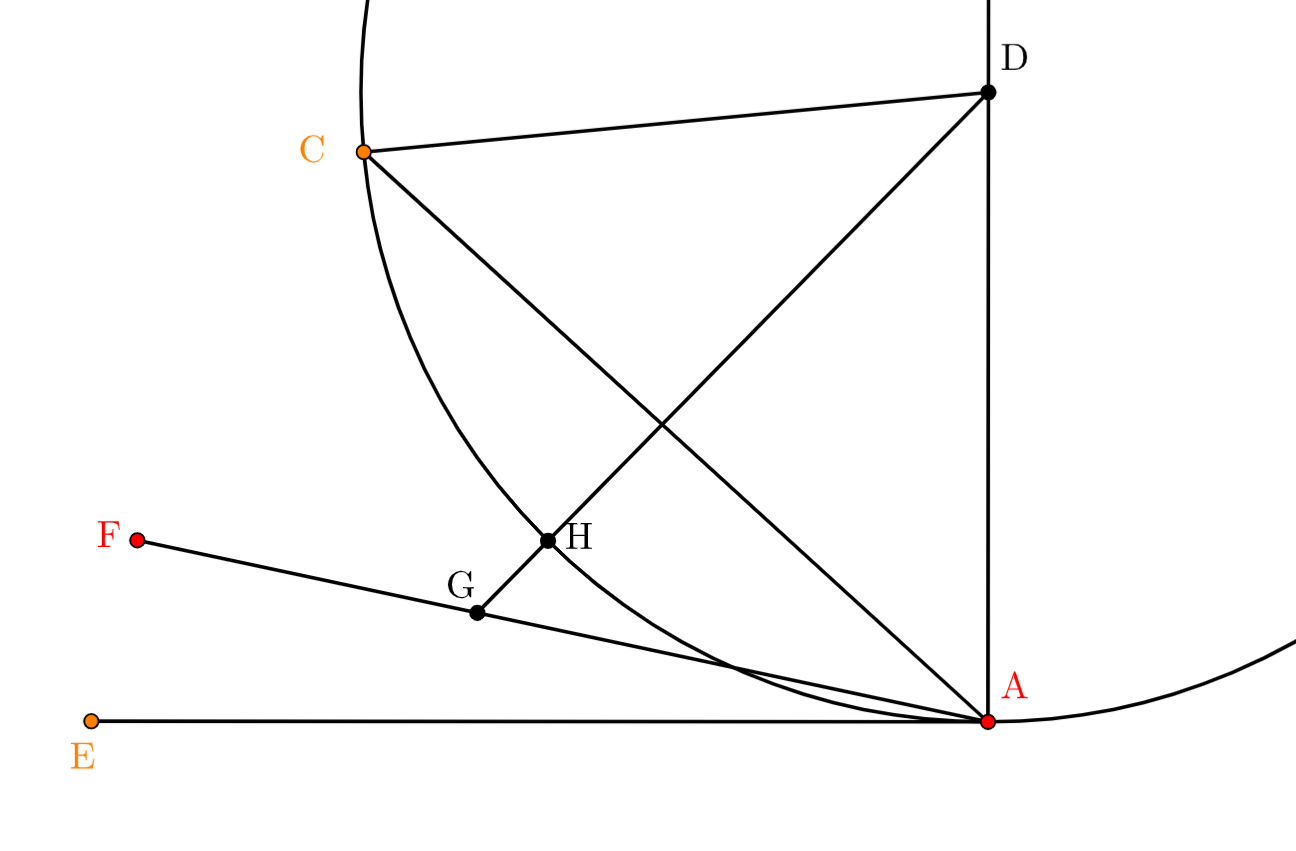
좌측 정도 크기의 사진이 내가 책에서 본 그림이다. 뿔각은 너무나 뾰족해서 더 이상 어떤 선분도 그 사이에 들어갈 틈이 없다고 했는데, 그림상 버젓이 FA 선분이 EA직선 사이에 들어가 있지 않은가. 그래서 직접 작도를 해봤다. 사이즈를 좀더 크게 그렸다. 그러자 숨어 있던 간극이 드러났다. FA는 EA 직선과 원 사이를 비집고 들어간 것이 아니라 원 안을 침범하고 있었다!! 신기해서 더 작게 그렸더니 정말 감쪽같이 FA 선분이 그 사이를 비집고 들어간 것처럼도 보이는 것을 다시 확인했다. ㅎㅎ 그러고 나서야 이 긴 지문의 명제가 의미하는 바를 겨우 알 수 있었다. 원과 접선 사이는 어떤 선분도 들어갈 수 없다!! 그만큼 이 뿔각은 가장 작은 예각이다. 현재 이 각은 쓰이지 않는다.
2) 여기서 무한소 개념과 미적분학의 기초가 시작되었다고 한다. 이것이 현재 쓸모 없는 각이지만 우리가 주목해야 할 이유이다. 이것은 접선의 역사에서 중요한 정리라고 한다.(131p 주석) 무한소란 미분의 기본 개념으로, 무한대로 쪼개서 작아진 것을 의미하는데, 과연 이 접선과 무한소는 어떻게 연결되는 걸까?
칸토어는 "선분과 선분이 접하면, 그게 아무리 짧을지라도, 서로 일치하게 되니 각이 생기지 않는다"고 했다. 접하는 각은 각이 아니라는 의미이다. 왜냐하면 접하는 원과 일치하기 때문이다. 그렇다면 접하는 점A는 무엇인가. 점은 부분이 아니기 때문에 선도 면도 아니며, 선과 면의 시작일 뿐이다. 따라서 이들이 만나는 점에서는 각을 만들 수 없다는 것. 각이 아니라 굽은 정도, 즉 곡률을 구하고 비교할 수 있다는 설명이다. 주석에서는 원의 접선 개념이 곡선에 대한 접선 개념으로 확장되었고, 이후 무한소 논쟁을 거쳐 17세기 말 라이프니츠와 뉴턴에 의해 미적분학의 기초가 되었다는 설명이다. 이 명제가 그 긴 여정의 출발점이라는 것. 다시 유클리드 1권의 정의들, 점선면으로 돌아간 셈이다. 삼각형이 아니라 점선면은 위대하다고 해야 하나? ㅎㅎ
안타깝게도 오늘 단기수학세미나 마지막이지만, 이 명제가 왜 무한소 개념의 출발점인지에 대해 이보다 더 구체적으로 파악할 수는 없었다. 우리는 다시 한 번 <원론> 책의 구성 뒷편 제10권의 무리수와 이후 11, 12, 13권으로 이어지는 공간기하까지 가보면 좀더 이런 설명을 이해할 수 있지 않을까 가늠해보았다. 매년 여름 조금씩 읽으면 3년정도 걸리지 않을까? 나의 질문에 곰곰이 답했다. "난 수학이 아니라 계산이 싫은 거였어! " 이렇게 여름은 끝났다.
| 번호 | 제목 | 작성자 | 작성일 | 조회 |
| 487 |
<세계 끝의 버섯> 2부 후기
(6)
호수
|
2023.12.28
|
조회 208
|
호수 | 2023.12.28 | 208 |
| 486 |
<세계 끝의 버섯> 1회차 후기
(3)
동은
|
2023.12.26
|
조회 273
|
동은 | 2023.12.26 | 273 |
| 485 |
<세계 끝의 버섯> 번개세미나 모집합니다! (4회)
(11)
동은
|
2023.11.26
|
조회 880
|
동은 | 2023.11.26 | 880 |
| 484 |
<기하학원론> 아홉번 째 후기 - 삼각형은 위대하다
(2)
여울아
|
2023.10.04
|
조회 173
|
여울아 | 2023.10.04 | 173 |
| 483 |
<기하학원론> 여덟번째 후기 - 이제 '원'인가요
(1)
곰곰
|
2023.09.25
|
조회 187
|
곰곰 | 2023.09.25 | 187 |
| 482 |
<기하학원론>일곱번째 후기-작도는 상상이 아니다
(3)
여울아
|
2023.09.19
|
조회 219
|
여울아 | 2023.09.19 | 219 |
| 481 |
<기하학원론> 여섯번째 후기
(3)
진공묘유
|
2023.09.12
|
조회 216
|
진공묘유 | 2023.09.12 | 216 |
| 480 |
<청년, 루크레티우스를 만나다> 저자 민호와의 만남의 자리! 후기입니다~
(2)
동은
|
2023.09.06
|
조회 222
|
동은 | 2023.09.06 | 222 |
| 479 |
<기하학원론> 다섯번째 후기
(2)
곰곰
|
2023.09.04
|
조회 201
|
곰곰 | 2023.09.04 | 201 |
| 478 |
<기하학 원론> 네 번째 후기 - 연속의 원리
여울아
|
2023.08.29
|
조회 156
|
여울아 | 2023.08.29 | 156 |
| 477 |
<청년, 루크레티우스를 만나다> 저자와의 만남에 초대합니다~ (8/31)
(2)
고은
|
2023.08.24
|
조회 806
|
고은 | 2023.08.24 | 806 |
| 476 |
<기하학 원론> 세번째 후기
(2)
진공묘유
|
2023.08.22
|
조회 178
|
진공묘유 | 2023.08.22 | 178 |

진공묘유님과 곰곰님 덕분에 유클리드 원론의 맛을 아주 쬐끔 봤습니다. 감사합니다. 고맙습니다~~~
ㅎㅎㅎ 눈 반짝반짝하면서 너무 재미있다, 놀랍다를 연발하시던 우리 여울아 반장님 ㅋㅋ 저야말로 덕분에 유클리드를 봤네요. 비록 원론 분량으로는 미약하지만... 그래도 아무도 안 살 것 같은, 도대체 창고에서 얼마나 오래 썩고 있었는지 냄새마저 구린 해설서를 3권이나 읽고... (쓰담쓰담) 다들 수고 많으셨습니다!